Detailed Description

Enables integration using metadynamics, a free energy technique.

The command integrate.mode_metadynamics sets up MD integration with an arbitrary integration method (such as NVT), to continuously samples the collective variables and uses their values to update the bias potential, from which forces are calculated.

Some features of this package are loosely inspired by the PLUMED plugin for Metadynamics, http://www.plumed-code.org/.

The metadynamics algorithm is reviewed in detail in Barducci et al., Metadynamics, Wiley Interdiscipl. Rev.: Comput. Mol. Sci. 5, pp. 826-843 (2011)

Explictly, the metadynamics biasing potential 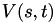$V(s,t)$ at time 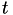$t$ takes the form

$V(\mathbf{s}, t) = \sum\limits_{t'=0, t_G, 2 t_G,\dots}^{t'<t} W e^{-\frac{V[\mathbf{s}(\mathbf{r}(t')]}{\Delta T}} \exp\left\{-\sum\limits_{i=1}^d \frac{[s_i(\mathbf{r}) - s_i(\mathbf{r}(t'))]^2}{2\sigma_i^2}\right\},$

where

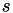is the vector of collective variables
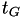is the stride (in time units). It should be chosen on the order of several 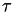$\tau$ , where 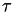$\tau$ is a typical internal relaxation time of the system.
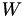is the height of Gaussians added during the simulation (in energy units).
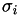$\sigma_i$ is the standard deviation of Gaussian added for collective variable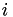

Before a metadynamics run, the collective variables need to be defined and the integration methods need to specified. Currently, the only collective variable available is

cv.lamellar

While metadynamics in principle works independently of the integration method, it has thus far been tested with

integrate.nvt

only.

During a metadynamics run, the potential is updated every 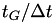$t_G/\Delta t$ steps and forces derived from the potential are applied to the particles every step.

The result of a metadynamics run is either a hills file (which contains the positions and heights of Gaussians that are added together to form the bias potential), or a bias potential evaluated on a grid. The negative of the bias potential can be used to calculate the free energy surface (FES).

By default, integrate.mode_metadynamics uses the well-tempered variant of metadynamics, where a shift temperature 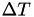$\Delta T$ is defined, which converges to a well-defined bias potential after a typical time for convergence that depends entirely on the system simulated and on the value of 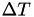$\Delta T$ . The latter quantity should be chosen such that 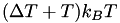$(\Delta T + T) k_B T$ equals the typical height of free energy barriers in the system.

By contrast, standard metadynamics does not converge to a limiting potential, and thus the free energy landscape is 'overfilled'. Standard metadynamics corresponds to 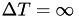$\Delta T = \infty$ . If the goal is to approximate standard metadynamics, large values (e.g. 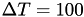$\Delta T = 100$ ) of the temperature shift can therefore be used.

Note:: The collective variables need to be defined before the first call to run(). They cannot be changed after that (i.e. after run() has been called at least once), since the integrator maintains a history of the collective variables also in between multiple calls to the run() command. The only way to reset metadynamics integration is to use another integrate.mode_metadynamics instance instead of the original one.

Two modes of operation are supported:

Resummation of Gaussians every time step
Evaluation of the bias potential on a grid

In the first mode, the integration will slow down with increasing simulation time, as the number of Gaussians increases with time.

In the second mode, a current grid of values of the collective variables is maintained and updated whenever a new Gaussian is deposited. This avoids the slowing down, and this mode is thus preferrable for long simulations. However, a reasonable of grid points has to be chosen for accuracy (typically on the order of 200-500, depending on the collective variable and the system under study).

It is possible to output the grid after the simulation, and to restart from the grid file. It is also possible to restart from the grid file and turn off the deposition of new Gaussians, e.g. to equilibrate the system in the bias potential landscape and measure the histogram of the collective variable, to correct for errors.

Note:: Grid mode is automatically enabled when it is specified for all collective variables simultaneously. Otherwise, it has to be disabled for all collective variables at the same time.

See also:: metadynamics.cv

In the following, we give an example for using metadynamics in a diblock copolymer system.

This sets up metadynamics with Gaussians of height 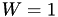$ W =1 $ (in energy units), which are deposited every 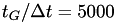$t_G/\Delta t=5000$ steps ( 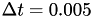$\Delta t = 0.005$ in time units), with a well-tempered metadynamics temperature shift 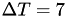$\Delta T = 7$ (in temperature units). The collective variable is a lamellar order parameter. At the end of the simulation, the bias potential is saved into a file.

 all = group.all
 meta = metadynamics.integrate.mode_metadynamics(dt=0.005, W=1,stride=5000, deltaT=dT)
 # Use the NVT integration method 
 integrate.nvt(group=all, T=1, tau=0.5)
 # set up a collective variable on a grid
 lamellar = metadynamics.cv.lamellar(sigma=0.05, mode=dict(A=1.0, B=-1.0), lattice_vectors=[(0,0,3)], phi=[0.0])
 lamellar.enable_grid(cv_min=-2.0, cv_max=2.0, num_points=400)
 # Run the metadynamics simulation for 10^5 time steps
 run(1e5)
 # dump bias potential
 meta.dump_grid("grid.dat")

If the saved bias potential should be used to continue the simulation from, this can be accomplished by the following piece of code

 meta = metadynamics.integrate.mode_metadynamics(dt=0.005, W=1,
 integrate.nvt(group=all, T=1, tau=0.5)
 # set up a collective variable on a grid
 lamellar = metadynamics.cv.lamellar(sigma=0.05, mode=dict(A=1.0, B=-1.0), lattice_vectors=[(0,0,3)], phi=[0.0])
 lamellar.enable_grid(cv_min=-2.0, cv_max=2.0, num_points=400)
 
 # restart from saved bias potential
 meta.restart_from_grid("grid.dat")
 run(1e5)

Inheritance diagram for mode_metadynamics:

[legend]

List of all members.

Public Member Functions
def	__init__
	Specifies the metadynamics integration mode.
def	update_forces
def	dump_grid
	Dump information about the bias potential If a grid has been previously defined for the collective variables, this method dumps the values of the bias potential evaluated on the grid points to a file, for later restart or analysis.
def	restart_from_grid
	Restart from a previously saved grid file This command may be used before starting the simulation with the run() command.
def	set_params
	Set parameters of the integration.

Public Attributes
	cpp_integrator
	supports_methods
	cv_names

Constructor & Destructor Documentation

def __init__	(	self,
		dt,
		W,
		stride,
		deltaT,
		filename = `""`,
		overwrite = `False`,
		add_hills = `True`
	)

Specifies the metadynamics integration mode.

Parameters:

dt	Each time step of the simulation run() will advance the real time of the system forward by dt (in time units)
W	Height of Gaussians (in energy units) deposited
stride	Interval (number of time steps) between depositions of Gaussians
deltaT	Temperature shift (in temperature units) for well-tempered metadynamics
filename	(optional) Name of the log file to write hills information to
overwrite	(optional) True if the hills file should be overwritten
add_hills	(optional) True if Gaussians should be deposited during the simulation

Member Function Documentation

def dump_grid	(	self,
		filename
	)

Dump information about the bias potential If a grid has been previously defined for the collective variables, this method dumps the values of the bias potential evaluated on the grid points to a file, for later restart or analysis.

This method can be used after the simulation has been run.

Parameters:

filename The file to dump the information to

def restart_from_grid	(	self,
		filename
	)

Restart from a previously saved grid file This command may be used before starting the simulation with the run() command.

Upon start of the simulation, the supplied grid file is then read in and used to initialize the bias potential.

Parameters:

filename The file to read, which has been previously generated by dump_grid

def set_params	(	self,
		add_hills = `True`
	)

Set parameters of the integration.

Parameters:

add_hills True if new Gaussians should be added during the simulation

The documentation for this class was generated from the following file:

integrate.py

Detailed Description

Public Member Functions

Public Attributes

Constructor & Destructor Documentation

Member Function Documentation